Desigualdad triangular

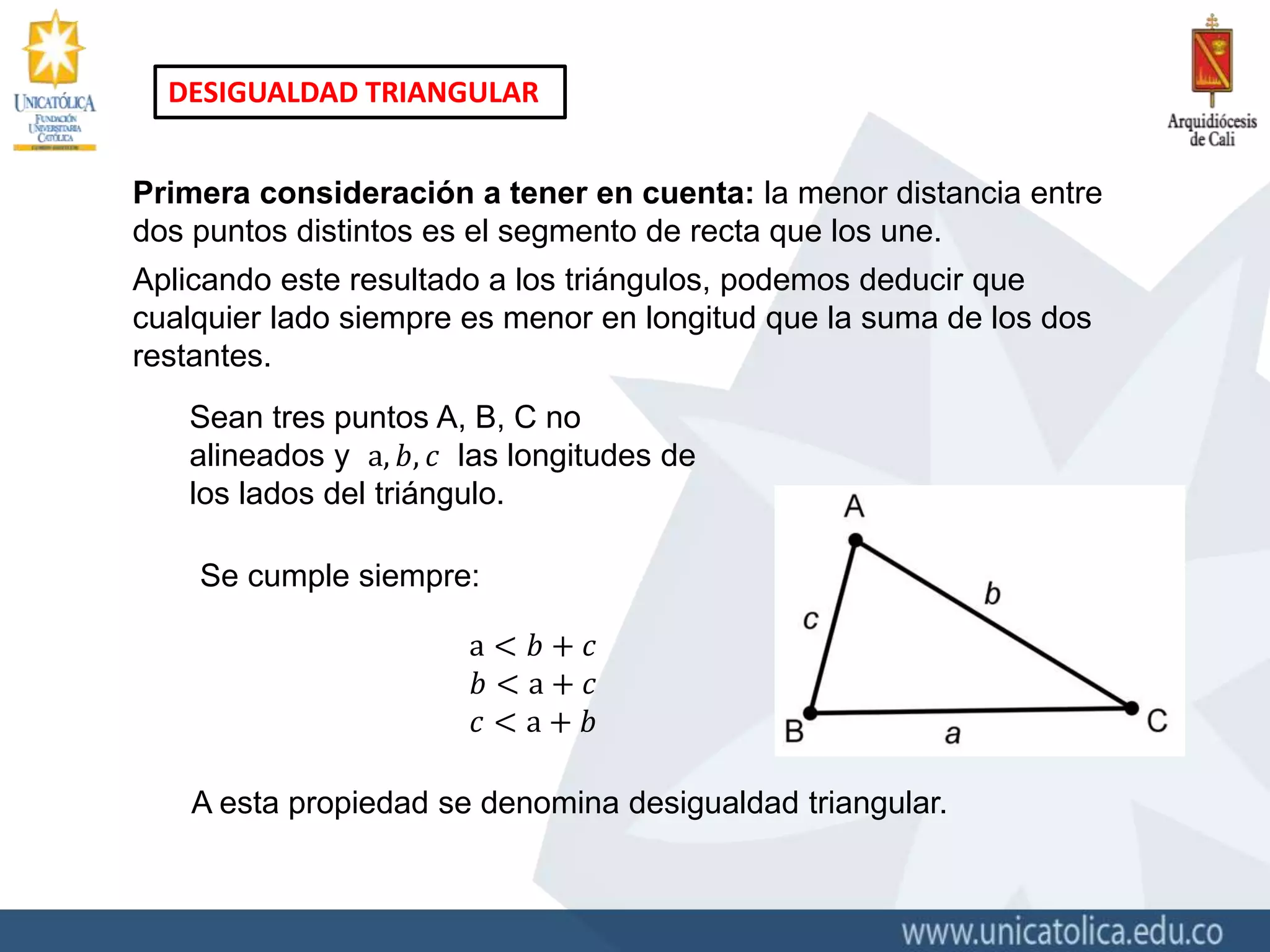
La desigualdad triangular es un teorema de geometría euclidiana que establece:

Este resultado ha sido generalizado a otros contextos más sofisticados como espacios vectoriales. Definido matemáticamente, cualquier triángulo cumple la siguiente propiedad:

${\displaystyle a<(b c),\qquad b<(a c),\qquad c<(a b)}$

donde a, b y c son los lados.

Espacios vectoriales normados

El teorema se pide como axioma para definir los espacios vectoriales normados (espacios vectoriales donde hay una norma ${\displaystyle \|\cdot \|}$ definida), resultando en la siguiente versión de la desigualdad triangular:

En particular, la recta real es un espacio vectorial normado con el valor absoluto como norma. Entre otras condiciones, se satisface la desigualdad triangular:

cuya demostración es:

Demostración

(Ámbito → ℝ). Haciendo uso de las propiedades del valor absoluto, es posible escribir:

${\displaystyle -|a|\leq a\leq |a|}$

${\displaystyle -|b|\leq b\leq |b|}$

Sumando ambas inecuaciones:

${\displaystyle -(|a| |b|)\leq a b\leq |a| |b|}$

A su vez, usando la propiedad de valor absoluto ${\displaystyle |c|\leq d}$ si y solo si ${\displaystyle -d\leq c\leq d}$ en la línea de arriba queda:

${\displaystyle |a b|\leq |a| |b|}$

Generalización de la desigualdad triangular para cualquier número de sumandos

La desigualdad triangular puede generalizarse a un número arbitrario de sumandos:

${\displaystyle |x_{1} x_{2} \cdots x_{n}|\leq |x_{1}| |x_{2}| \cdots |x_{n}|}$,

es decir:

${\displaystyle \left|\sum _{i=1}^{n}x_{i}\right|\leq \sum _{i=1}^{n}|x_{i}|.}$

donde n es un número natural, y los ${\displaystyle x_{i}}$ son números reales.

Desigualdad de Minkowski

La desigualdad triangular puede generalizarse aún más para integrales (Riemann, Riemann-Stieltjes, Lebesgue-Stieltjes, etc):

${\displaystyle \left|\int _{A}f(x){\text{d}}\mu (x)\right|\leq \int _{A}|f(x)|{\text{d}}\mu (x)}$

así como también para espacios L^p. Sea S un espacio medible, sea 1 ≤ p ≤ ∞ y sea f y g elementos de L^p(S). Entonces f g es de L^p(S), y se tiene

${\displaystyle \|f g\|_{p}\leq \|f\|_{p} \|g\|_{p}}$

con la igualdad para el caso1 < p < ∞ si y sólo si f y g son positivamente linealmente dependientes (que significa que f = λg o g = λf para algún λ ≥ 0).

Esta desigualdad se llama desigualdad de Minkowski y está demostrada en su propio artículo. Igual que la desigualdad de Hölder, la desigualdad de Minkowski se puede especificar para sucesiones y vectores haciendo:

${\displaystyle \left(\sum _{k=1}^{n}|x_{k} y_{k}|^{p}\right)^{1/p}\leq \left(\sum _{k=1}^{n}|x_{k}|^{p}\right)^{1/p} \left(\sum _{k=1}^{n}|y_{k}|^{p}\right)^{1/p}}$

para todos los números reales (o complejos) x₁, ..., x_n, y₁, ..., y_n y donde n es el cardinal de S (el número de elementos de S).

Véase también

• Desigualdad de Cauchy-Schwarz

Notas

Bibliografía

• Hardy, G., Littlewood J.E., Polya, G. (1999). Inequalities, Cambridge Mathematical Library, Cambridge University Press. ISBN 0-521-05206-8
• H. Minkowski, Geometrie der Zahlen , Chelsea, reprint (1953)
• M.I. Voitsekhovskii (2001), "Minkowski inequality", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1-55608-010-4